Venturi Meter as a Bernoulli Principle Example
The Venturi meter is a classical and practical example of the Bernoulli’s principle applied to real fluid flow. It consists of a converging section, a throat, and a diverging section installed along a pipe.
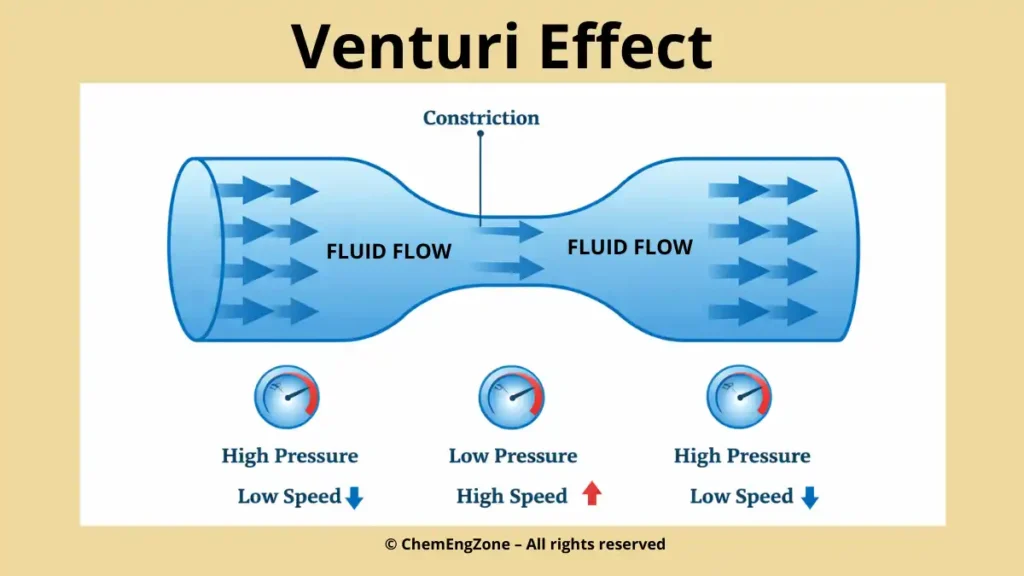
Venturi meter diagram: velocity increases and static pressure decreases at the constriction, in accordance with Bernoulli’s principle.
As the fluid enters the converging section, the cross-sectional area decreases and the velocity increases. According to Bernoulli’s principle, this increase in kinetic energy is accompanied by a decrease in static pressure. The minimum pressure occurs at the throat, where the velocity reaches its maximum value.
By measuring the pressure difference between an upstream section and the throat, the flow velocity — and consequently the volumetric flow rate — can be determined. In this way, the Venturi meter directly converts the energy balance expressed by Bernoulli’s equation into a measurable quantity.
The Venturi meter clearly illustrates how pressure, velocity, and geometry are intrinsically linked through mechanical energy conservation. It also shows why pressure measurements alone are insufficient without considering velocity and cross-sectional area.
Venturi meter equation
By combining Bernoulli’s principle with the continuity equation, the pressure difference measured between the upstream section and the throat can be related to the volumetric flow rate.
For an ideal Venturi meter, the volumetric flow rate can be expressed as:
where is the cross-sectional area at the throat, is the pressure difference between the upstream section and the throat, is the fluid density, and the diameter ratio.
This expression shows that the measured pressure difference is directly linked to the flow rate through the geometry of the Venturi meter and the fluid properties.
Use of Venturi Meters in Chemical Engineering Practice
In chemical engineering, Venturi meters are widely used for reliable flow measurement in process lines where robustness and low energy losses are required. They are commonly installed on liquid, gas, and steam lines to monitor and control mass and volumetric flow rates in continuous processes.
A key advantage of the Venturi meter is its low permanent pressure loss compared to other differential pressure devices. This makes it particularly suitable for applications where energy efficiency is critical or where pressure margins are limited, such as recirculation loops, utility systems, and large-diameter pipelines.
Venturi meters are often preferred in dirty or multiphase services, where suspended solids, fouling, or droplets may be present. Unlike sharp-edged devices, the smooth converging–diverging geometry reduces erosion and minimizes measurement drift over time.
From an operational perspective, the Venturi meter provides a stable and repeatable signal that can be directly integrated into control systems. The measured pressure difference is converted into a flow rate and used for process monitoring, mass balance calculations, and flow control strategies.
Limitations and Practical Considerations
Although the Venturi meter is derived from Bernoulli’s principle, its application in real systems requires accounting for non-ideal effects. Real flows are not inviscid, and viscous effects introduce irreversible energy losses that are not included in the ideal Bernoulli equation. As a result, the actual flow rate deviates from the theoretical prediction.
These deviations are handled at the instrumentation level through the discharge coefficient. The coefficient provides an empirical correction to the ideal equation, accounting for losses related to meter geometry, surface finish, and Reynolds number. Its value is obtained through experimental calibration and is required for accurate flow measurement.
Installation conditions introduce an additional source of uncertainty. Flow disturbances generated upstream by valves, bends, or fittings can distort the velocity profile entering the Venturi, affecting the measured pressure difference. For this reason, adequate straight pipe lengths upstream and downstream are required to ensure reliable operation.
From a system perspective, these requirements define the practical limits of Venturi meter applicability. Size, installation constraints, and cost may limit their use in small-diameter lines or compact layouts. In addition, services involving severe multiphase flow or highly compressible fluids may require alternative flow-measurement technologies.
Conclusion
The Venturi meter is a practical example of Bernoulli’s principle, showing how a pressure difference generated by a controlled constriction can be converted into a flow rate. Its value lies not in ideal behavior, but in making the mechanical energy balance directly observable.
This example illustrates a core engineering principle: pressure, velocity, and geometry must always be interpreted together within an energy balance applied to a real system.
Ing. Ivet Miranda
⬆️ Back to TopVenturi Meter – Check Your Understanding
A Venturi meter is installed on a process line and connected to a differential pressure transmitter. What does the instrument actually measure?
Other Articles You May Find Useful
- First Law of Thermodynamics and Joule’s Experiment
- Second Law of Thermodynamics: PM 2nd Kind
- Fluid Dynamics Basics for Engineers
- Heat Transfer Basics for Engineers
- Unit Operations: A Practical Introduction for Engineers
- What Does a Chemical Engineer Do in Industrial Environments?
- Chemical Engineering Core Disciplines – A Practical Overview
FAQ
What does a Venturi meter measure to determine flow?
A Venturi meter does not measure flow directly. It measures the pressure difference between an upstream section and the throat of the meter. This pressure difference is then converted into flow rate using Bernoulli’s principle and the continuity equation.
How does a venturi meter work
A Venturi meter works by accelerating the fluid through a constriction, creating a pressure drop. This pressure difference is measured and converted into flow rate using Bernoulli’s principle and continuity.
Why does a Venturi meter cause a pressure drop?
A Venturi meter causes a pressure drop because the fluid accelerates as it passes through the constricted throat. According to Bernoulli’s principle, an increase in velocity corresponds to a decrease in static pressure. This pressure drop is not a loss of energy, but a conversion of pressure energy into kinetic energy, which is then used to determine the flow rate.