3. Law of Poiseuille: Viscous Flow in Pipes

What the Law of Poiseuille Describes

The law of Poiseuille describes how viscous forces control fluid flow in pipes under laminar conditions. It explains why a pressure gradient is required to sustain motion and how viscosity, pipe geometry, and pressure drop determine the volumetric flow rate.

In previous articles on fluid dynamics, the fundamental concepts used to describe fluid motion were introduced. Steady flow, streamlines, and mass conservation were analysed, together with the relationship between pressure, velocity, and elevation described by Bernoulli’s principle for ideal fluids.

Bernoulli’s equation explains how mechanical energy is redistributed in an ideal, inviscid flow. Poiseuille’s law extends this framework to real fluids by accounting for viscous dissipation and by quantifying the energy that must be continuously supplied to maintain motion.

When viscous effects are taken into account, pressure no longer remains constant along a pipe, even when velocity and geometry do not change. This is the physical context in which Poiseuille’s law applies.

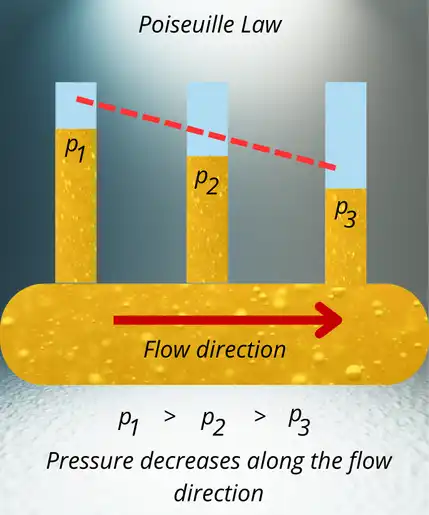
Pressure Loss in Laminar Pipe Flow

Figure 1 illustrates this behaviour for a steady laminar flow in a horizontal pipe with constant cross-section. Static pressure measured by piezometers decreases progressively along the flow direction, such that p₁ > p₂ > p₃.

The pressure decrease shown in the figure is not a transient effect and is not caused by changes in velocity or elevation. The flow is steady, and the pipe geometry remains unchanged along its length. The pressure gradient exists solely because viscous forces continuously dissipate mechanical energy as the fluid flows. To maintain steady motion, this energy loss must be compensated by a continuous pressure drop along the pipe.

Effect of viscosity on real fluids

Viscosity generates internal friction both between adjacent fluid layers and between the fluid and the pipe wall. This internal friction continuously dissipates mechanical energy as the fluid flows.

As a consequence, pressure cannot remain constant along the pipe. A progressive pressure decrease is required to compensate for viscous energy losses and to maintain steady motion.

Access the FREE PDF – Poiseuille Law Visual Explanation

Download a one-page A4 visual summary explaining why pressure decreases along a pipe in laminar flow. The PDF illustrates viscous energy dissipation, head loss, and the physical meaning of the law of Poiseuille using clear diagrams and engineering reasoning.

Continue to Access the PDF

This behavior is directly observable using piezometers along a horizontal pipe: evenly spaced pressure taps show a linear drop in fluid height, indicating uniform head loss in steady laminar flow.

Head loss in steady pipe flow

The progressive pressure decrease along the pipe is known as head loss.

In laminar flow:

• the pressure gradient is constant
• head loss is proportional to fluid viscosity
• the loss is distributed uniformly along the pipe length

This regime allows an exact analytical solution.

Law of Poiseuille: when it applies

If the following conditions are satisfied:

• Newtonian fluid
• incompressible flow
• fully developed laminar regime
• Reynolds number typically Re < 2000
• pipe length much larger than its diameter

the volumetric flow rate can be calculated using Poiseuille’s law:

$$Q = \frac{\pi R^4}{8 \mu L}\,\Delta P$$where:

• $Q$ = volumetric flow rate
• $R$ = pipe radius
• $\mu$ = dynamic viscosity
• $L$ = pipe length
• $\Delta P$ = pressure drop

This equation shows the strong dependence of flow rate on pipe radius and viscosity.

To sustain this steady flow despite viscous energy dissipation, an external energy input is required. In practical systems, this energy is supplied by a pressure difference generated by devices such as pumps.

Engineering relevance

Law of Poiseuille explains why:

• small pipe diameters cause large pressure losses
• viscous fluids require significantly higher pumping power
• laminar flow is highly sensitive to viscosity

When flow becomes turbulent, this model is no longer valid and empirical correlations such as Darcy–Weisbach must be used.

Conclusion

Poiseuille’s law provides a clear physical interpretation of laminar pipe flow in real fluids. Unlike ideal flow models, it shows that viscosity continuously dissipates mechanical energy, making a pressure gradient unavoidable even in pipes with constant cross-section and steady velocity.

From an engineering standpoint, this law highlights the dominant role of viscosity, pipe length, and especially pipe radius in determining pressure losses and pumping requirements. The strong dependence on radius explains why small geometric changes can have a disproportionate impact on flow rate and energy consumption.

Although its validity is limited to fully developed laminar flow, Poiseuille’s law remains a fundamental reference. It establishes the conceptual bridge between ideal fluid dynamics and real industrial piping systems, and it provides the foundation upon which more general pressure-loss models are built when turbulence or complex flow conditions arise.

Ing. Ivet Miranda

Follow me on LinkedIn

⬆️ Back to Top

Related Process Safety & Risk Analysis Articles

1. Fluid Dynamics Basics for Engineers
2. Bernoulli’s Principle: Equation&Applications
3. Chemical Engineering Core Disciplines – A Practical Overview
4. First Law of Thermodynamics and Joule Experiment
5. Second Law of Thermodynamics: PM 2nd Kind

FAQ